安装Certbot

Certbot是一个自动生成Let’s Encrypt免费SSL证书的自由开源工具。CentOS可以通过yum直接安装：

1

yum install certbot

获取Cloudflare API Key

因为DNS解析是托管在CloudFlare上，通过DNS API去验证域名所有权并申请/更新证书操作起来更简单。

在CloudFlare个人资料里获取Global API Key，在VPS上创建cf.ini文件填入帐号和Key：

1
2
3

# Cloudflare API credentials used by Certbot
dns_cloudflare_email = [email protected]
dns_cloudflare_api_key = 0123456789abcdef0123456789abcdef0123

申请证书

用DNS插件申请域名和二级域名的证书：

1
2
3
4

certbot certonly -d 'yourdomain.com' -d '*.yourdomain.com' \
	--dns-cloudflare \
	--dns-cloudflare-credentials /etc/nginx/cf.ini \
	--dns-cloudflare-propagation-seconds 60

证书默认会保存在/etc/letsencrypt/live/yourdomain.com目录下面。

配置Nginx

配置/etc/nginx/nginx.conf：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

server {
    listen       443 ssl http2;
    listen       [::]:443 ssl http2;
    server_name  _;
    root         /usr/share/nginx/html;

    ssl_certificate      /etc/letsencrypt/live/yourdomain.com/fullchain.pem;
    ssl_certificate_key  /etc/letsencrypt/live/yourdomain.com/privkey.pem;

    ssl_session_cache shared:le_nginx_SSL:1m;
    ssl_session_timeout 1440m;
    ssl_session_tickets off;

    ssl_dhparam /etc/nginx/dhparam.pem;

    ssl_protocols TLSv1.2 TLSv1.3;
    ssl_prefer_server_ciphers on;
    ssl_ciphers HIGH:!aNULL:!eNULL:!EXPORT:!DES:!RC4:!MD5:!kRSA;
}

重启Nginx就对所有二级域名都生效了。可以到SSL Labs检测一下SSL评分是不是A+。

证书续期

证书有效期为90天，所以需要定期更新，离过期30天以内可以续期，续期命令（可以加--dry-run试一下）：

1
2
3
4

certbot renew \
	--dns-cloudflare \
	--dns-cloudflare-credentials /etc/nginx/cf.ini \
	--dns-cloudflare-propagation-seconds 60

可以写个crontab定时任务每个月执行一次：

1

55 7 1 * * /usr/bin/certbot renew --dns-cloudflare --dns-cloudflare-credentials /etc/nginx/cf.ini --dns-cloudflare-propagation-seconds 60 >> ~/cert.log && systemctl restart nginx

主路由使用N1盒子OpenWrt系统进行拨号以后，由于和光猫不在一个网段，下级设备无法直接通过192.168.1.1访问桥接过来的光猫了。之前使用Padavan的时候wan口接光猫时会作为光猫的DHCP客户端自动获取一个192.168.1.*的ip地址，下级设备都可以直接访问到光猫的地址；而OpenWrt却没有分配到光猫网段的地址，所以需要手动创建一个接口。

在网络-接口中创建一个新接口，名字可以叫man，协议选DHCP客户端，接口选择和wan口相同的接口，我这里是eth0.2。

创建后修改高级设置，禁用使用默认网关选项；在防火墙设置里，将防火墙区域选到wan上。

最后保存后去接口里连接MAN就会发现可以获取到192.168.1.*网段下的地址了，然后光猫就可以访问了。

获取固件

首先从恩山论坛上获取最新的flippy大神的固件，从网盘下载一般文件名为openwrt_s905d_n1_Rxx.xx.xx_kxx.xx.xx-flippy-xx+o.7z。

关于+和+o版本的区别请看作者的帖子。

解压后得到img文件，用Etcher或Rufus等工具烧录到U盘中。

U盘启动

U盘插到N1盒子上电，就应该能直接进入OpenWrt系统。

如果之前刷过电视盒子系统进不去U盘启动，可以先在原系统下连上局域网并查到ip，电脑上adb连接并重启：

adb connect 192.168.xxx.xxx
adb shell reboot update

应该就可以进入U盘系统了。

修改ip地址

有两种方法：

HDMI连接显示器

如果hdmi无信号有可能是4K显示器不支持换一台试试。
在显示的终端里编辑/etc/config/network，将lan的ipaddr改成想要的地址（如192.168.0.1）并保存。
执行/etc/init.d/network restart重启网络生效。

连接N1已开启的WiFi

接入盒子自带的无线网（SSID：Phicomm_n1 密码：password），浏览器访问openwrt/，修改网络-接口-LAN里的ip地址即可。

常规设置

刷入EMMC

可以选择继续用U盘启动，也可以执行sh /root/install-to-emmc.sh选择刷入盒子的内置闪存，刷入之前最好用ddbr命令备份一下。

配置WAN口

在网络-接口里设置WAN接口（没有就添加一个），宽带拨号就用PPPoE协议；物理设置的接口自定义成eth0.2，因为只有一个网口，连到了交换机上的VLAN2上和光猫进行桥接；最后给wan配置防火墙。

配置LAN口

协议就是上面设置的静态地址；物理设置指定桥接接口，选中eth0和无线网络；给lan配置防火墙。

下面的DHCP服务器高级设置中选中动态DHCP和强制作为局域网内唯一的DHCP服务器。

禁用IPv6 DNS

在网络-DHCP/DNS中的高级设置中禁止解析 IPv6 DNS 记录，防止在科学上网时梯子只支持IPv4的情况。

其他

开启UPnP

在服务-UPnP里开启，当在局域网里挂一些PCDN服务时会用到。

网络加速

在网络-Turbo ACC 网络加速里可以适当打开流量分载和BBR。

N1盒子装上Armbian以后就可以当作一台低功耗的小主机使用，配合各种docker可以集各种功能于一体。

刷入Armbian

Armbian固件使用的是恩山flippy大神的49+o（原帖地址），目前已经稳定，于是在刷入u盘后顺手刷入了eMMC。

在刷入前先在u盘启动的系统里运行ddbr命令选b进行备份（记得选压缩），文件保存到了/ddbr目录，以便以后有需要时恢复原系统。
然后执行install-to-emmc.sh脚本按提示将系统拷贝到N1的闪存中。拷贝完成关机、拔U盘、再开机，就进入内置的系统了。

安装docker

执行install-docker.sh安装docker，啪的一下就安装完成了，很快啊！

可以接着安装一个Docker图像化管理工具Portainer：

1
2

docker volume create portainer_data
docker run -d --name portainer --restart always -p 9000:9000 -v /var/run/docker.sock:/var/run/docker.sock -v portainer_data:/data portainer/portainer

安装OpenWrt

OpenWrt的Docker镜像使用的也是flippy大神提供的（原帖地址），目前还在更新。

启动容器

从网盘上下载压缩包传到Armbian目录下，省去pull的步骤直接启动：

1
2
3

gzip -dc docker-img-openwrt-aarch64-r20.10.20.gz | docker load
docker network create -d macvlan --subnet=192.168.123.0/24 --gateway=192.168.123.1 -o parent=eth0 macnet
docker run -d --name openwrt --restart always --network macnet --privileged unifreq/openwrt-aarch64:r20.10.20

配置OpenWrt地址

执行docker exec -it openwrt bash进入容器里进行配置。
编辑容器里的/etc/config/network配置文件，将option ipaddr的值改为指定给OpenWrt的ip地址，如192.168.123.2。
保存后执行/etc/init.d/network restart使配置生效。
此时通过浏览器访问刚刚配置的地址应该就可以进入luci管理界面了（默认密码应该是password）。

旁路由设置

通过浏览器进入OpenWrt的管理界面，在网络-接口里修改lan的配置，将IPv4网关设置为主路由的地址，如192.168.123.1，在使用自定义的DNS服务器里添加几个当地最好用的公共DNS；在物理设置里关闭桥接接口；关闭DHCP服务器里的动态DHCP功能，保存并与应用设置。

主路由设置

在主路由的内部网络(LAN)-DHCP服务器设置里将默认网关和DNS服务器设置为旁路由地址，如192.168.123.2。
如果主路由是padavan固件且外部网络(WAN)-外网设置开启了硬件加速，需要将IPv4 硬件加速设置为OFFLOAD TCP/UDP for LAN。

Armbian和OpenWrt网络互通

按照上面设置完旁路由发现Docker的宿主机Armbian系统和OpenWrt无法互相访问。需要修改Armbian网络配置/etc/network/interfaces，增加如下内容：

1
2
3
4
5
6
7
8
9
10

up ip link set eth0 promisc on

auto macvlan
iface macvlan inet static
    address 192.168.123.123
    netmask 255.255.255.0
    gateway 192.168.123.1
    dns-nameservers 192.168.123.1
    pre-up ip link add macvlan link eth0 type macvlan mode bridge
    post-down ip link del macvlan link eth0 type macvlan mode bridge

保存后执行systemctl restart networking使配置生效，两个地址就可以互相访问了。

然后在比硬路由更强大的N1盒子上就起一些留学服务了。

MacBook升级后去掉了USB口，插移动硬盘比较麻烦，所以就一直没有备份时间机器了。后来觉得samba挂载的硬盘也可以用来备份，于是就想起了2019年捡垃圾时在某宝买的蜗牛星际矿渣（现在挂上硬盘装了OMV系统成为了一台家用NAS），希望可以无线局域网的环境下直接备份。

OMV设置

配置共享文件夹

首先进入OMV控制台配置一个共享文件夹用于Time Machine的备份：

这里我用了单独一块磁盘用于备份，并把文件夹命名为Backup。

配置完成后在特权里给用于备份的账户授予读写权限，并更改ACL设置如下：

更改samba设置

以root身份登入OMV，编辑samba的配置文件/etc/samba/smb.conf，更改备份文件夹的内容：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

[Backup]
comment = Time Machine
path = /srv/dev-disk-by-label-Backup/
guest ok = no
guest only = no
read only = no
browseable = yes
inherit acls = yes
inherit permissions = no
ea support = no
store dos attributes = no
fruit:encoding = private
fruit:locking = none
fruit:metadata = netatalk
fruit:resource = file
fruit:time machine = yes
vfs objects = catia fruit streams_xattr
printable = no
create mask = 0664
force create mode = 0664
directory mask = 0775
force directory mode = 0775
hide special files = yes
follow symlinks = yes
hide dot files = yes
valid users = "shintaku"
invalid users =
read list =
write list = "shintaku"

主要变化在于更改了vfs objects的值并增加了几个fruit的配置。

保存后运行testparm看一下配置是否正确，没问题就可以systemctl restart smbd重启服务了。

macOS设置

将Mac和NAS放到统一局域网下，用Finder的前往-连接服务器挂载一下备份硬盘看看是否正常。

开启文件共享

进入系统偏好设置-共享，在文件共享的选项里将SMB共享打勾：

配置时间机器

进入系统偏好设置-时间机器，点选择磁盘：

发现在NAS上配置的共享磁盘已经出现了，选择这个磁盘会弹出窗口认证身份，填入之前授权过的用户名密码即可：

然后就连接完成，可以开始备份了：

2019年6月初由于某事件发生30周年，导致某长城突然加高，将大量机场IP屏蔽，于是将梯子改成了v2ray，并通过cloudflare代理DNS解析的方式将翻墙流量伪装成对域名的tls访问流量，曲线解决了IP端口被封的问题。
但是路由器上使用v2ray客户端有一些性能问题，总觉得不如原来的shadowsocks流畅，于是找到一种继续使用ss，并通过v2ray-plugin插件来伪装流量的方法。

服务端

搭建服务

停用原来的python版，安装shadowsocks-libev：

yum install shadowsocks-libev -y

克隆v2ray-plugin代码并编译（需要golang环境）：

git clone https://github.com/shadowsocks/v2ray-plugin.git
cd v2ray-plugin && go build
cp v2ray-plugin /usr/bin/

更改配置

编辑/etc/shadowsocks-libev/config.json：

1
2
3
4
5
6
7
8
9
10

{
    "server":"0.0.0.0",
    "server_port":23333,
    "local_port":1080,
    "password":"password",
    "timeout":300,
    "method":"rc4-md5",
    "plugin":"v2ray-plugin",
    "plugin_opts":"server;loglevel=none"
}

本来这里使用v2ray插件的目的是将shadowsocks的流量伪装成tls流量，自然服务器端口应当使用443。
但是我的服务器同时还启用了nginx，再使用443会造成端口冲突，所以在这里使用一个其他的端口，然后再用nginx做一次端口转发。

端口转发

在/etc/nginx/conf.d/目录下新建一个配置：

1
2
3
4
5
6
7
8
9
10
11
12
13

server {
    listen       443;
    server_name  ss.your.domain;

    location / {
        proxy_pass http://127.0.0.1:23333;
        proxy_redirect      off;
        proxy_http_version  1.1;
        proxy_set_header    Host $http_host;
        proxy_set_header    Upgrade $http_upgrade;
        proxy_set_header    Connection "upgrade";
    }
}

server_name需要使用自己的域名，并将这个二级域名解析到vps上。

保存后重启nginx，启动shadowsocks并设置开机启动：

systemctl restart nginx
systemctl start shadowsocks-libev
systemctl enable shadowsocks-libev

客户端

主要注意以下配置：

• 服务器地址填上面配置的二级域名
• 服务器端口填443
• 插件名称填v2ray-plugin
• 插件参数填tls;host=二级域名

路由器

此处以老毛子固件为例：

打开开关应用即可。

Windows

• 客户端下载：shadowsocks-windows
• 插件下载：v2ray-plugin

下载完成将插件v2ray-plugin.exe解压到shadowsocks的文件夹中（使其与shadowsocks.exe平级），启动按如下配置：

macOS

• 客户端下载：ShadowsocksX-NG

将客户端解压到应用目录（客户端会自己安装插件），启动按如下配置：

Android

• 客户端下载：shadowsocks-android
• 插件下载：v2ray-plugin-android

两个apk安装以后启动按如下配置：

最近手贱将Hexo的博客的版本升到了3.8.0，顺便将npm组件也都升级了。一开始没有发现什么问题，后来打开一篇带公式的文章发现里面的部分MathJax公式渲染失败了。想到之前曾经因为Markdown里面的下划线_表示斜体，和MathJax里的下标冲突了，之前改过的node_modules被更新覆盖了，这次索性重新搞一遍。

更换渲染引擎

卸载原来的hexo-renderer-marked，换成专门对MathJax魔改过的hexo-renderer-kramed（注意kram这个单词的拼写）：

npm uninstall hexo-renderer-marked --save
npm install hexo-renderer-kramed --save

再安装hexo-renderer-mathjax渲染器：

npm install hexo-renderer-mathjax --save

更改字符集

为了避免语义冲突，修改node_modules/kramed/lib/rules/inline.js文件的escape和em：

1
2

//escape: /^\\([\\`*{}\[\]()#$+\-.!_>])/,
escape: /^\\([`*\[\]()#$+\-.!_>])/,

1
2

//em: /^\b_((?:__|[\s\S])+?)_\b|^\*((?:\*\*|[\s\S])+?)\*(?!\*)/,
em: /^\*((?:\*\*|[\s\S])+?)\*(?!\*)/,

更改cdn链接

修改node_modules/hexo-renderer-mathjax/mathjax.html的最后一行，将http改成https：

1
2

<!--script src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script-->
<script src="https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script>

这样是为了避免在网站为https协议时请求http的内容时被浏览器block。使用hexo s预览是否已生效。

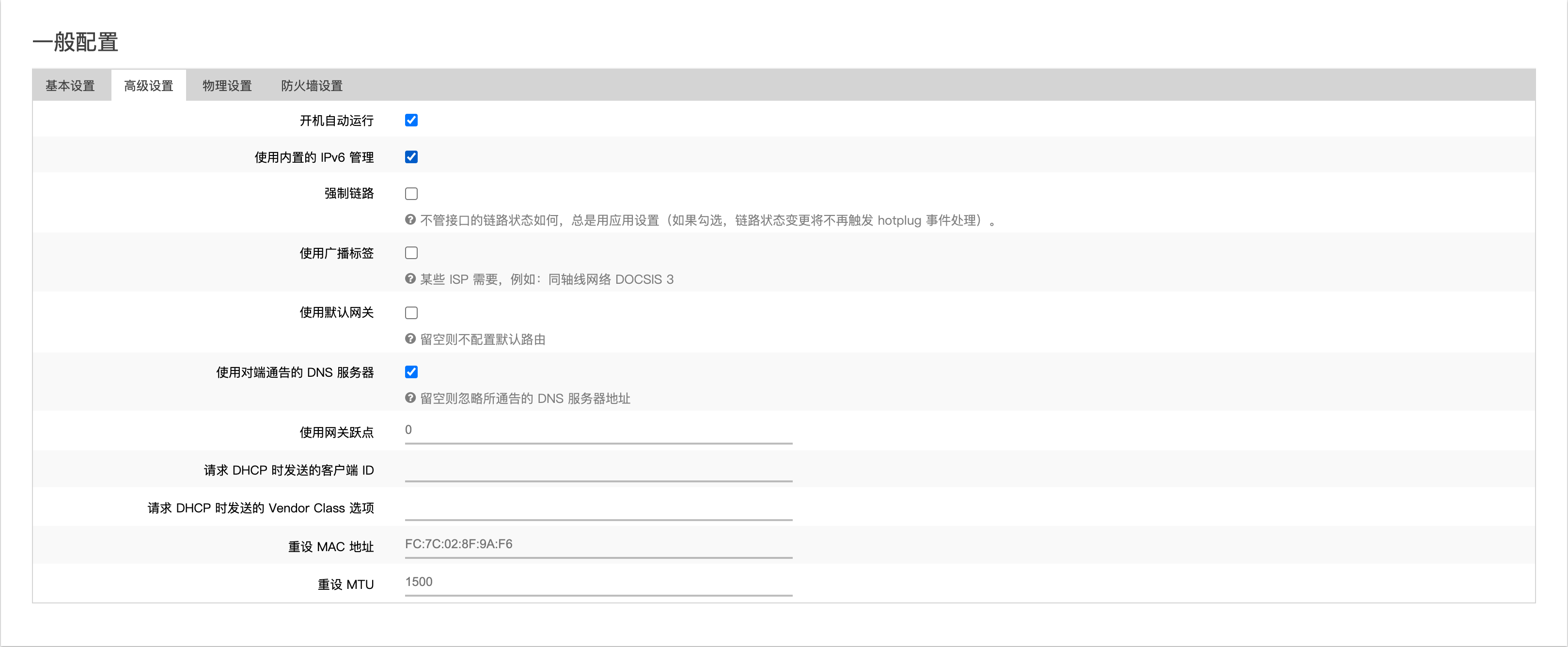
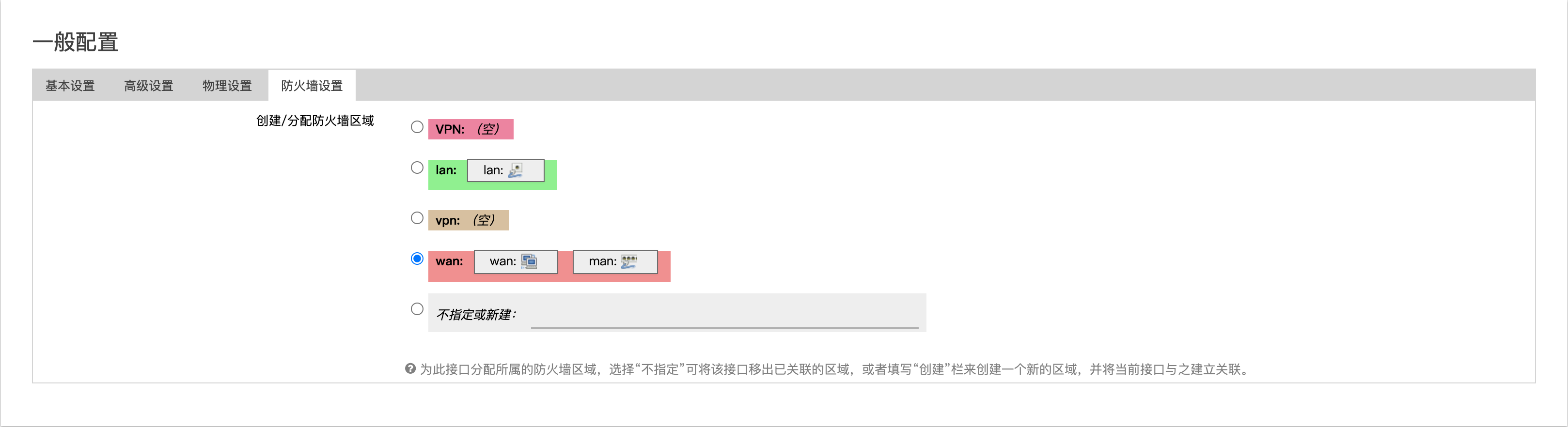
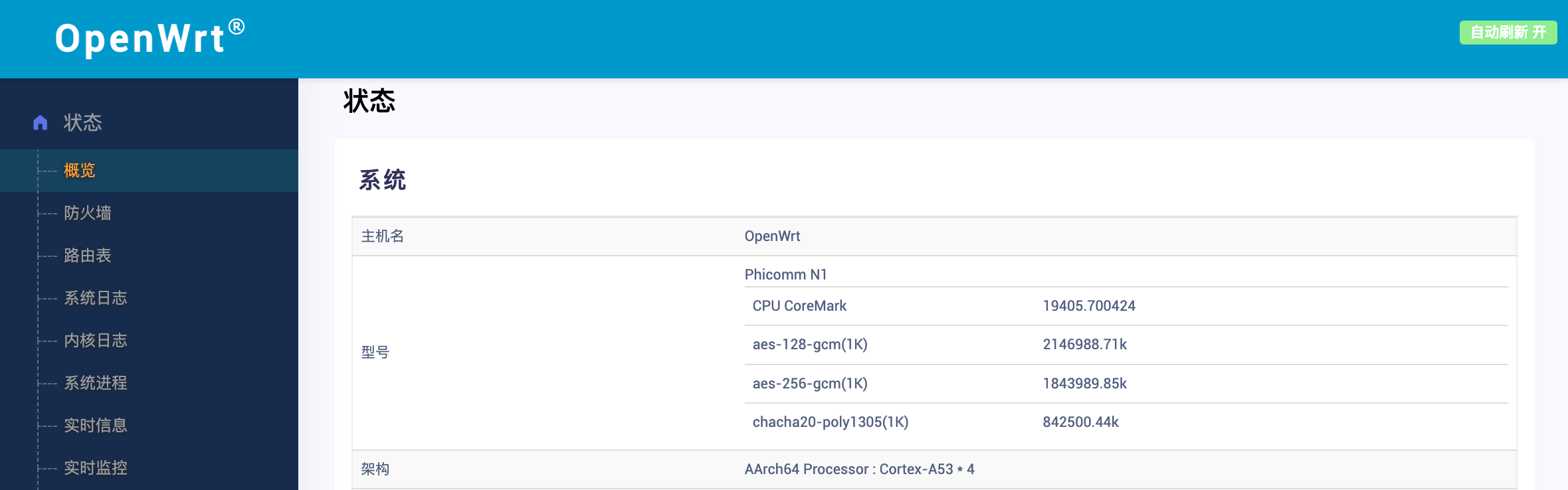
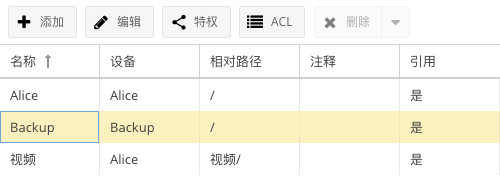
之前偶然拿到一台大麦DW22D路由器，应该是之前的租客办长城宽带赠送的，登入管理界面发现里面是基于长城宽带深度定制的系统。

上了恩山查了一下发现这个机器的硬件还可以，并且可以无拆机刷入padavan固件，所以就开始按照教程刷机。

无拆机刷机

以下步骤参考恩山的教程。

开启ssh

本方法主要依靠后门页面的命令注入漏洞，步骤如下：

注入新密码

电脑连上路由器（最好有线方式），访问http://192.168.10.1/upgrade.html，在页面上打开ssh的选项，密码框内输入：

123 | echo 6c216b27c8c9b051106c969e2077d4e9 > /ezwrt/bin/upgrade_passwd 

注意末尾有空格。这里的md5值是echo dfc643 | md5算出来的，里面的dfc643是发现这个方法大佬的用户名，此处的密码是可以随便改的。然后点确定提交，此时会提示密码错误，可以忽略。

注入ssh公钥

再次访问http://192.168.10.1/upgrade.html，同样选择打开ssh，密码框内输入：

123 | echo YOUR_ID_RSA_PUB > /etc/dropbear/authorized_keys 

同样注意末尾有空格。其中YOUR_ID_RSA_PUB替换为自己的公钥，即电脑上~/.ssh/id_rsa.pub的内容。再次点确定提交，此时还会提示密码错误，也可以忽略。

开启ssh

最后一次访问http://192.168.10.1/upgrade.html，选择打开ssh，密码为dfc643（如果在第一步注入密码时用了别的密码，此处输入相应的密码），最后点确定提交，提示start ssh success表示已经开启ssh。

这样就可以ssh [email protected]登录路由器了。

刷入breed

breed是hackpascal独立开发的一个全新的 Bootloader。DW22D路由器对应的版本是breed-mt7620-reset13.bin。

下载好后将其传入路由器的/tmp目录下备用：

scp breed-mt7620-reset13.bin [email protected]:/tmp

然后在路由器上执行：

mtd_write -x mIp2osnRG3qZGdIlQPh1 -r write /tmp/breed-mt7620-reset13.bin bootloader

这样应该就能将breed刷入bootloader，然后就可以随意刷firmware了。

然而我手残将最后的bootloader打成了firmware，也就是将breed刷入了firmware分区，导致路由器进不去系统了，也才有了后面的ttl救砖。

TTL刷机

以下步骤参考恩山的教程。

USB转TTL

为了让路由器硬件和电脑相连，需要一个USB转TTL模块，随便在马云家买一个最便宜的就能用，我就买了一个ch340g芯片的模块。

TTL驱动

然后在github找了驱动安装上（这里给的是Mac电脑的驱动，Windows的驱动一般卖家都会提供，网上找找也都有）。

重启后打开网络偏好可以看见多了一个串行接口：

将USB转TTL模块插在电脑上，在/dev目录下会出现名字类似cu.usbserial-1410的设备，说明识别成功。

TTL连接

在如图位置焊上引脚（GND那个孔不用焊）：

然后用杜邦线将三个引脚和USB转TTL模块相连。

开启TFTP

将电脑用网线和路由器lan口连接，设置有线连接为手动模式，按图修改参数：

参考macOS启用TFTP服务，将breed-mt7620-reset13.bin放到TFTP目录下，将TFTP的地址选择有线ip（即上面设置的10.10.10.3）。

刷机

一切就绪后，可以连接路由器开始刷机。

登录路由器

使用screen连接未通电的路由器，波特率为57600：

screen /dev/cu.usbserial-1410 57600

此时终端里什么也没有。然后给路由器通电，此时会打印出很多东西，最后出现一些选项，立刻（5秒内）按数字键9选择TFTP刷机。

刷入breed

之后会让确认device IP（路由器地址）和server IP（电脑地址），确认无误后会提示输入要刷入的文件名，输入breed-mt7620-reset13.bin回车就开始刷入了。

刷完后断电按住复位键通电并长按5秒即可进入breed：

TFTP在路由器刷机中被普遍使用，因为其协议简单，可以通过少量存储器实现。在PC上打开Windows功能就可启用。其实macOS也自带TFTP，只不过是没有自动启用。

TFTP默认使用的目录是/private/tftpboot，首先给其增加权限：

sudo chmod -R 777 /private/tftpboot

然后启用服务：

sudo launchctl load -F /System/Library/LaunchDaemons/tftp.plist
sudo launchctl start com.apple.tftpd

如果觉得命令行方式不直观，macOS上也有类似Windows上的Tftpd32的应用TFTP Server，直接下载安装即可：

TFTP的目录也可以在应用中修改。

之前曾经介绍过SoftEthern VPN的搭建，最近换了新的VPS，需要重新搭建VPN，由于除了iOS以外的其他平台都可以用ShadowSocks的梯子，就想搭建一个最简单的无需安装第三方App的VPN给iOS使用。想到系统自带的VPN可以连接L2TP over IPSec，就决定搭一个L2TP的VPN。

由于新VPS装的是CentOS 6，所以CentOS 7风格的命令就写在注释里了。

安装

先安装openswan和xl2tpd：

yum install openswan xl2tpd

如果没有ppp也要安装。

配置IPSec

在/etc/ipsec.d中新建一个vpn.conf文件，内容如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

conn L2TP-PSK-NAT
    rightsubnet=vhost:%priv
    also=L2TP-PSK-noNAT

conn L2TP-PSK-noNAT
    authby=secret
    pfs=no
    auto=add
    keyingtries=3
    rekey=no
    ikelifetime=8h
    keylife=1h
    type=transport
    left=YOUR_PUBLIC_IP_ADDRESS
    leftprotoport=17/1701
    right=%any
    rightprotoport=17/%any

其中left的值改为VPS的公网IP。

再新建一个vpn.secrets文件，里面写一行：

1

YOUR_PUBLIC_IP_ADDRESS %any: PSK "YOUR_PRE_SHARED_KEY"

前面还是公网IP，后面引号里面是自己设置的预共享密钥。

更改系统参数

编辑/etc/sysctl.conf文件，修改或添加成以下配置：

1
2
3
4
5
6
7
8
9
10

net.ipv4.ip_forward = 1
net.ipv4.conf.default.rp_filter = 0
net.ipv4.conf.all.send_redirects = 0
net.ipv4.conf.default.send_redirects = 0
net.ipv4.conf.all.log_martians = 0
net.ipv4.conf.default.log_martians = 0
net.ipv4.conf.default.accept_source_route = 0
net.ipv4.conf.all.accept_redirects = 0
net.ipv4.conf.default.accept_redirects = 0
net.ipv4.icmp_ignore_bogus_error_responses = 1

用sysctl -p命令使更改生效。

然后用以下脚本将/proc/sys/net/ipv4/conf下配置的值都改为0：

1
2
3
4
5

for each in /proc/sys/net/ipv4/conf/*
do
    echo 0 > $each/accept_redirects
    echo 0 > $each/send_redirects
done

启动IPSec

启动IPSec并加入开机启动：

service ipsec start        #systemctl start ipsec
chkconfig ipsec on        #systemctl enable ipsec

然后用ipsec verify检查一下是否配置正确，正常如下：

Version check and ipsec on-path                           [OK]
Libreswan 3.15 (netkey) on 4.12.9-1.el6.elrepo.x86_64
Checking for IPsec support in kernel                      [OK]
 NETKEY: Testing XFRM related proc values
     ICMP default/send_redirects                          [OK]
     ICMP default/accept_redirects                        [OK]
     XFRM larval drop                                     [OK]
Pluto ipsec.conf syntax                                   [OK]
Hardware random device                                    [N/A]
Two or more interfaces found, checking IP forwarding      [OK]
Checking rp_filter                                        [OK]
Checking that pluto is running                            [OK]
 Pluto listening for IKE on udp 500                       [OK]
 Pluto listening for IKE/NAT-T on udp 4500                [OK]
 Pluto ipsec.secret syntax                                [OK]
Checking 'ip' command                                     [OK]
Checking 'iptables' command                               [OK]
Checking 'prelink' command does not interfere with FIPSChecking for obsolete ipsec.conf options                  [OK]
Opportunistic Encryption                                  [DISABLED]

如果有异常请检查之前的配置。

配置xl2tpd

编辑/etc/xl2tpd/xl2tpd.conf配置如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

[global]
listen-addr = YOUR_PUBLIC_IP_ADDRESS
ipsec saref = yes

[lns default]
ip range = 192.168.1.128-192.168.1.254
local ip = 192.168.1.99
require chap = yes
refuse pap = yes
require authentication = yes
name = LinuxVPNserver
ppp debug = yes
pppoptfile = /etc/ppp/options.xl2tpd
length bit = yes

其实主要注意监听地址和几个yes就行了，其他基本不用动。

然后编辑/etc/ppp/options.xl2tpd配置如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

ipcp-accept-local
ipcp-accept-remote
ms-dns	8.8.8.8
ms-dns	8.8.4.4
noccp
auth
crtscts
idle 1800
mtu 1410
mru 1410
nodefaultroute
debug
lock
proxyarp
connect-delay 5000

在/etc/ppp/chap-secrets里添加帐号密码：

1
2
3

# client	server	secret			IP addresses
username1	*	password1		*
username2	*	password2		*

按照对应格式填上帐号密码即可。

启动xl2tpd并加入开机启动：

service xl2tpd start        #systemctl start xl2tpd
chkconfig xl2tpd on        #systemctl enable xl2tpd

最后在本地设备上填上地址、预共享密钥、用户名、密码就可以连接了。